![]()
The Hardy-Weinberg theorem characterizes the distributions of genotype frequencies in populations that are not evolving, and is thus the fundamental null model for population genetics.

Under the now-discredited theory of blending inheritance, the hereditary material was conceived as a fluid that combines the traits from two individuals into phenotypically intermediate offspring. Given observed patterns of resemblance between parents and offspring, blending inheritance may seem intuitively reasonable, as it did to many of Charles Darwin’s contemporaries. This mode of inheritance, however, posed problems for Darwin’s theory of natural selection (1859), which depends on the existence of heritable trait variation in populations of organisms. Blending inheritance would quickly erode such variation, since all traits would be combined from one generation to the next until all individuals shared the same blended phenotype. In his famous experiments on pea plants, Gregor Mendel rejected this hereditary mechanism in favor of particulate inheritance by demonstrating that alternative versions of genes (alleles) account for variations in inherited characters, though he didn’t actually know about genes as such. Although Mendel published his results in 1866, his work remained obscure until its rediscovery in 1900 (reviewed in Monaghan & Corcos 1984), which helped give rise to the modern field of genetics.
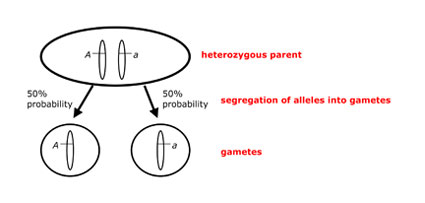
Mendel’s Law of Segregation, in modern terms, states that a diploid individual carries two individual copies of each autosomal gene (i.e., one copy on each member of a pair of homologous chromosomes). Each gamete produced by a diploid individual receives only one copy of each gene, which is chosen at random from the two copies found in that individual. Under Mendel’s Law of Segregation, each of the two copies in an individual has an equal chance of being included in a gamete, such that we expect 50% of an individual’s gametes to contain one copy, and 50% to contain the other copy (Figure 1).

An individual’s genotype is the combination of alleles found in that individual at a given genetic locus. If there are two alleles in a population at locus A (A and a), then the possible genotypes in that population are AA, Aa, and aa. Individuals with genotypes AA and aa are homozygotes (i.e., they have two copies of the same allele). Individuals with genotype Aa are heterozygotes (i.e., they have two different alleles at the A locus). If the heterozygote is phenotypically identical to one of the homozygotes, the allele found in that homozygote is said to be dominant, and the allele found in the other homozygote is recessive.
Even after many geneticists had accepted Mendel’s laws, confusion lingered regarding the maintenance of genetic variation in natural populations. Some opponents of the Mendelian view contended that dominant traits should increase and recessive traits should decrease in frequency, which is not what is observed in real populations. Hardy (1908; Figure 2) refuted such arguments in a paper that, along with an independently published paper by Weinberg (1908; Figure 3) laid the foundation for the field of population genetics (Crow 1999; Edwards 2008).

The Hardy-Weinberg Theorem deals with Mendelian genetics in the context of populations of diploid, sexually reproducing individuals. Given a set of assumptions (discussed below), this theorem states that:
If the genotype frequencies in a population deviate from Hardy-Weinberg expectations, it takes only one generation of random mating to bring them into the equilibrium proportions, provided that the above assumptions hold, that allele frequencies are equal in males and females (or else that individuals are hermaphrodites), and that the locus is autosomal. If allele frequencies differ between the sexes, it takes two generations of random mating to attain Hardy-Weinberg equilibrium. Sex-linked loci require multiple generations to attain equilibrium because one sex has two copies of the gene and the other sex has only one.
Given these conditions, it is easy to derive the expected Hardy-Weinberg genotype frequencies if we think about random mating in terms of the probability of producing each genotype via random union of gametes into zygotes (Table 1). If each allele occurs at the same frequencies in sperm and eggs, and gametes unite at random to produce zygotes, then the probability that any two alleles will combine to form a particular genotype equals the product of the allele frequencies. Since there are two ways of generating the heterozygous genotype (A egg and a sperm, or a egg and A sperm), we sum the probabilities of those two types of union to arrive at the expected Hardy-Weinberg frequency of the heterozygous genotype (2pq).

Table 1: A Punnett square depicting the probabilities of generating all possible genotypes at a diallelic Mendelian locus in a population that conforms to Hardy-Weinberg assumptions.
It is important to recognize that the Hardy-Weinberg equilibrium is a neutral equilibrium, which means that a population perturbed from its Hardy-Weinberg genotype frequencies will indeed reach equilibrium after a single generation of random mating (if it conforms to the other assumptions of the theorem), but it will be a new equilibrium if allele frequencies have changed. This property distinguishes a neutral equilibrium from a stable equilibrium, in which a perturbed system returns to the same equilibrium state. It makes sense that the Hardy-Weinberg equilibrium is not stable, since a change from the equilibrium genotype frequencies will generally be associated with a change in allele frequencies (p and q), which will in turn lead to new values of p 2 , 2pq and q 2 . Thereafter, a population that meets Hardy-Weinberg assumptions will remain at the new equilibrium until perturbed again.
Given a population in which we know the number of individuals with each genotype, we can test for statistical deviation from Hardy-Weinberg equilibrium using a simple chi-square goodness-of-fit test or a more powerful exact test. The latter class of methods has proved particularly useful for large-scale genomic studies, in which scientists evaluate thousands of loci segregating for multiple alleles (Wiggington et al. 2005). Observed genotype proportions in natural populations typically conform to Hardy-Weinberg expectations, as we might expect given that a population perturbed from equilibrium can achieve new equilibrium frequencies after only one generation of random mating.
Although statistical deviation from Hardy-Weinberg expectations generally indicates violation of the assumptions of the theorem, the converse is not necessarily true. Some forms of natural selection (e.g., balancing selection, which maintains multiple alleles in a population) can generate genotypic frequency distributions that conform to Hardy-Weinberg expectations. It may also be true that migration or mutation is occurring, but at such low rates as to be undetectable using available statistical methods. And, of course, all real populations are finite and thus susceptible to at least some evolution via genetic drift.